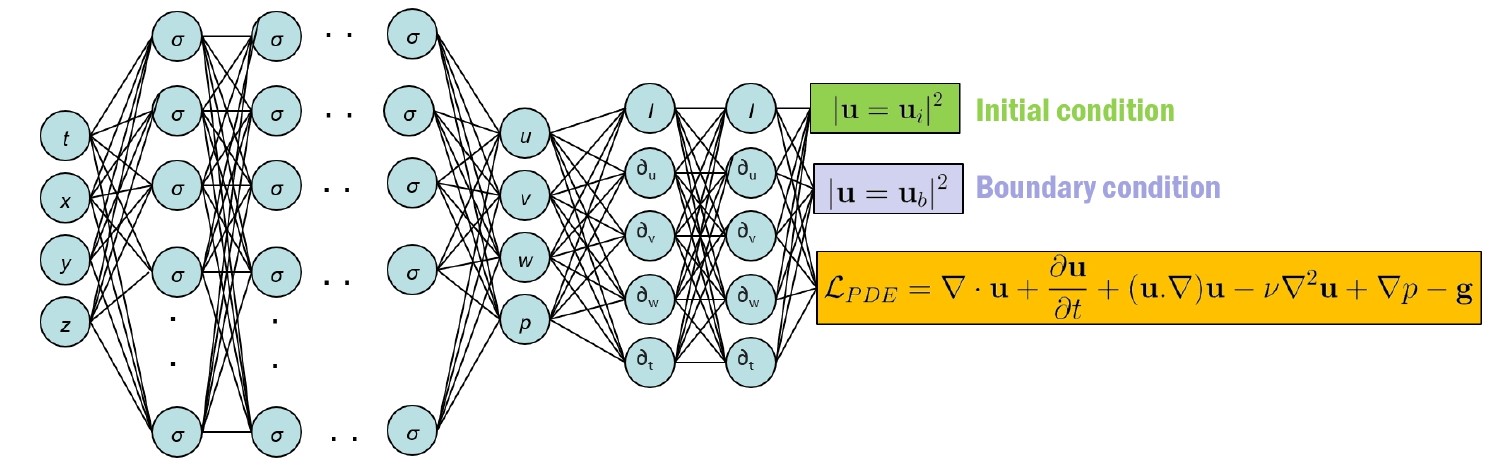
Physics Informed Neural Network incorporating Navier-Stokes Equation.
Data-driven Flow Prediction using Machine Learning
Our main focus on Data Driven Fluid Mechanics is to utilized machine learning methodologies for predicting complex heat and fluid flow behaviors. We develop and apply machine learning techniques for complex engineering modeling and design optimization purposes. Currently, we are working on the development of Physics Informed Neural Network (PINN) to model complex physical systems. PINN is a variant of Deep Neural Network (DNN) which incorporates the physical laws, such as the Navier-Stokes equation. The Figure below is an example of flow prediction obtained using our PINN model.
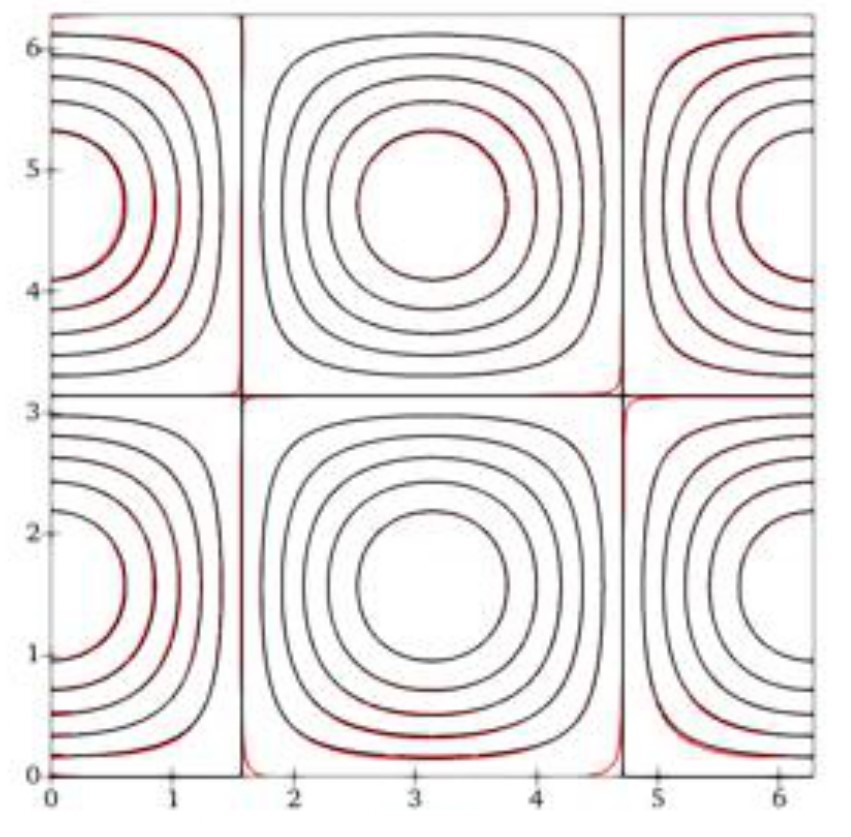
Taylor Green Vortex: Analytical (black) and PINN (Red).
One of the current research projects in this group is to utilize Explainable Neural Network methodologies for turbulence modeling. The Figure below is an example showing that our method surpasses benchmark conventional turbulence models in predicting the Reynolds stress of flow inside a square duct.
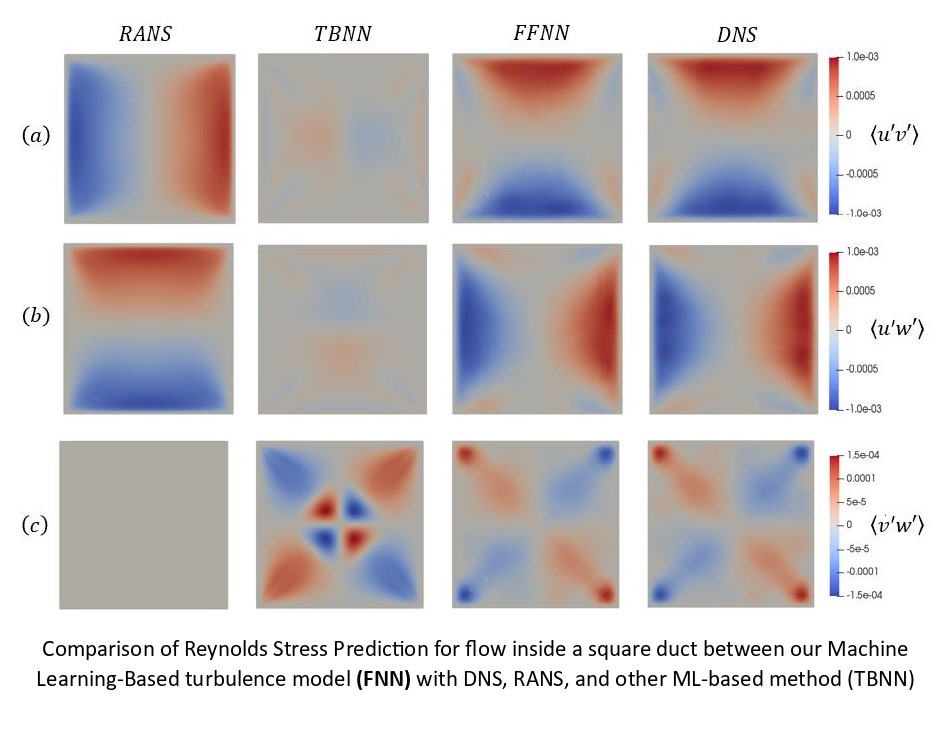
Explainable Neural Network-based turbulence modeling: Our Method (FNN).
Data-driven Surrogate Modeling and Optimization
Our group also develop data-driven methodologies for design optimization and design exploration of engineering problems by using Machine Learning (ML) and Statistical Learning algorithms such as Kriging/Gaussian Process (GP), Polynomial Chaos Expansion (PCE), and Support Vector Machine (SVM). Long story short, it will support the decision-making process and improve the development process of complex engineering products to obtain the best results. This research embraces both theory and applications perspectives. From the theoretical perspective, we develop codes and algorithms that could spur the advancement of machine learning technology. Whereas from the application perspective, we emphasize on multi-objective optimization, probabilistic design, inverse design and robust optimization that are significant to real-world engineering design problems.
From the application viewpoint, the researches that we have done include optimization of a flapping wing, experimental optimization of thrust performance of flexible caudal fin panels, multi-objective wind turbine shape optimization design, and structural topology optimization. From the algorithmic viewpoint, we have developed algorithms such as GP with composite kernel learning and gradient-enhanced polynomial chaos Kriging. Deep Learning is also used in data-driven surrogate modeling for Uncertainty Quantification of Random Fields.

Shape optimization of a wind turbine.
Shape optimization, or aerodynamic shape optimization in specific, has become our main interest since the first time. In this field, we successfully developed and implemented techniques and algorithms to efficiently alter the shape of geometry into the optimum configuration. One of the many cases that we have done is the aerodynamic shape optimization of NREL phase VI wind turbine geometry.
In that project, we implemented a multi-objective Bayesian optimization technique based on expected hypervolume improvement (EHVI) and high-fidelity computational fluid dynamics (CFD) was implemented for wind turbine shape design. A radial-basis function-based mesh deformation technique was applied to deform the baseline and obtain various optimized wind turbine geometries. The optimization framework is then applied to redesign the NREL Phase VI wind turbine geometry in order to optimize the torque and volume of the blade. Results showed that the optimization procedure was able to find optimized shapes.
We also had successfully implemented a multi-objective Bayesian optimization into aerodynamic shape optimization of transonic compressor by modifying the swept angle and the twist angle of the compressor’s blade. The result of the optimization are an increase in the compressor’s total pressure ratio (PR) and an increase in adiabatic efficiency.
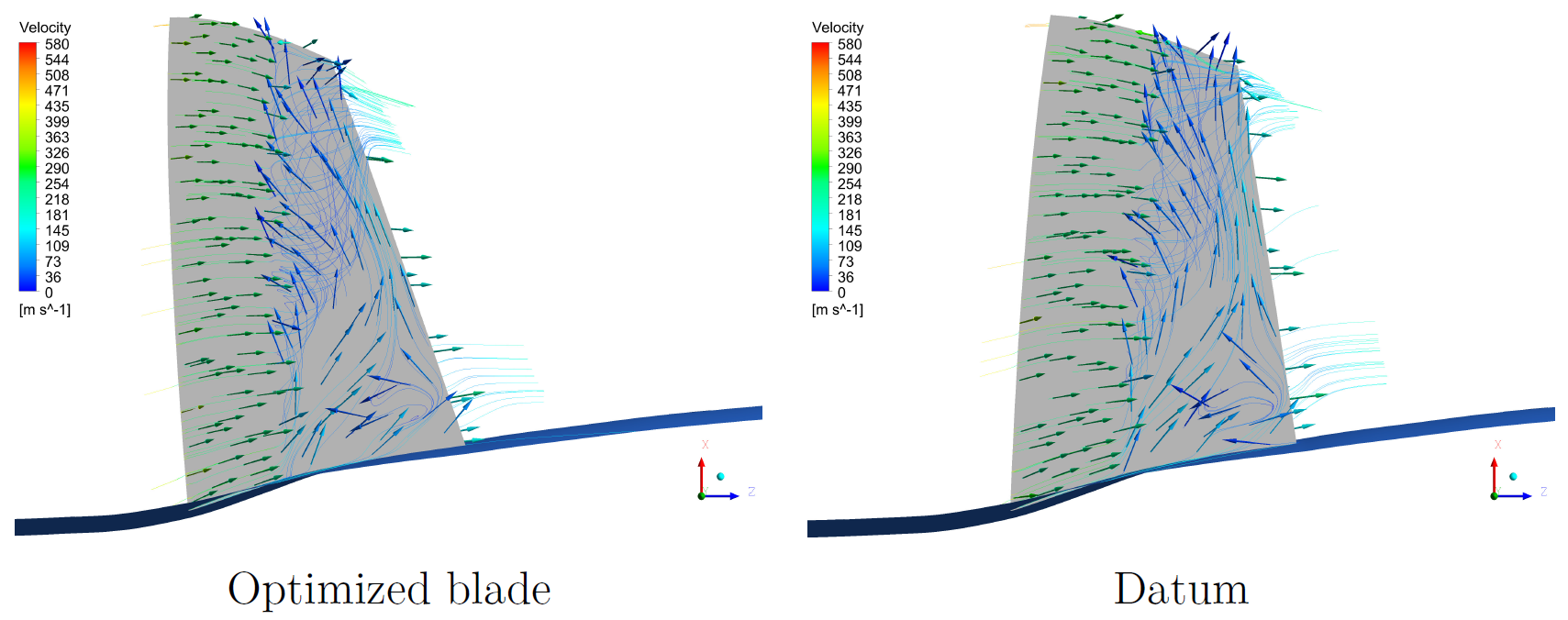
Optimized and datum compressor comparison.

Optimization of simple bridge structure.
Another research in this topic is topology optimization. Compared to shape optimization, topology optimization has a higher level of difficulty. Topology optimization is the most advanced one where not even a previous guess about the shape of boundaries of internal features is required. That, in turn, had led topology optimization to be an essential step in the conceptual design for structural design and is by now being extensively used in mechanical, automotive and aerospace industries throughout the world. The Figure above is an example of topology optimization result using our developed methodology.
Data-driven Method Development
Aside from research that focused on engineering application, we also conduct research that develops methods that enhance the performance of the conventional methods. Some of the algorithms that we successfully developed are Gaussian Process (GP) with composite kernel learning and gradient-enhanced polynomial chaos Kriging (GEPCK). The study shows that both algorithms outperform the conventional Gaussian Process in their test cases.

Examples of new kernels constructed by CKL (left). CKL outperforms existing kernels on the centrifugal diffuser problem (right).
GP with composite kernel learning (CKL) technique works by constructing a new kernel from the weighted sum combination of existing kernels where the weights and hyperparameters of Kriging are simultaneously trained. By deploying Kriging with CKL, we aim to better capture the input-output relationship of black-box functions in engineering design problems through the construction of more suitable kernels. We have successfully demonstrated the effectiveness of GP-CKL on several computational fluid dynamics problems. The results show that the Kriging with CKL generally outperforms or performs similarly to the best performing kernel on the two test problems.
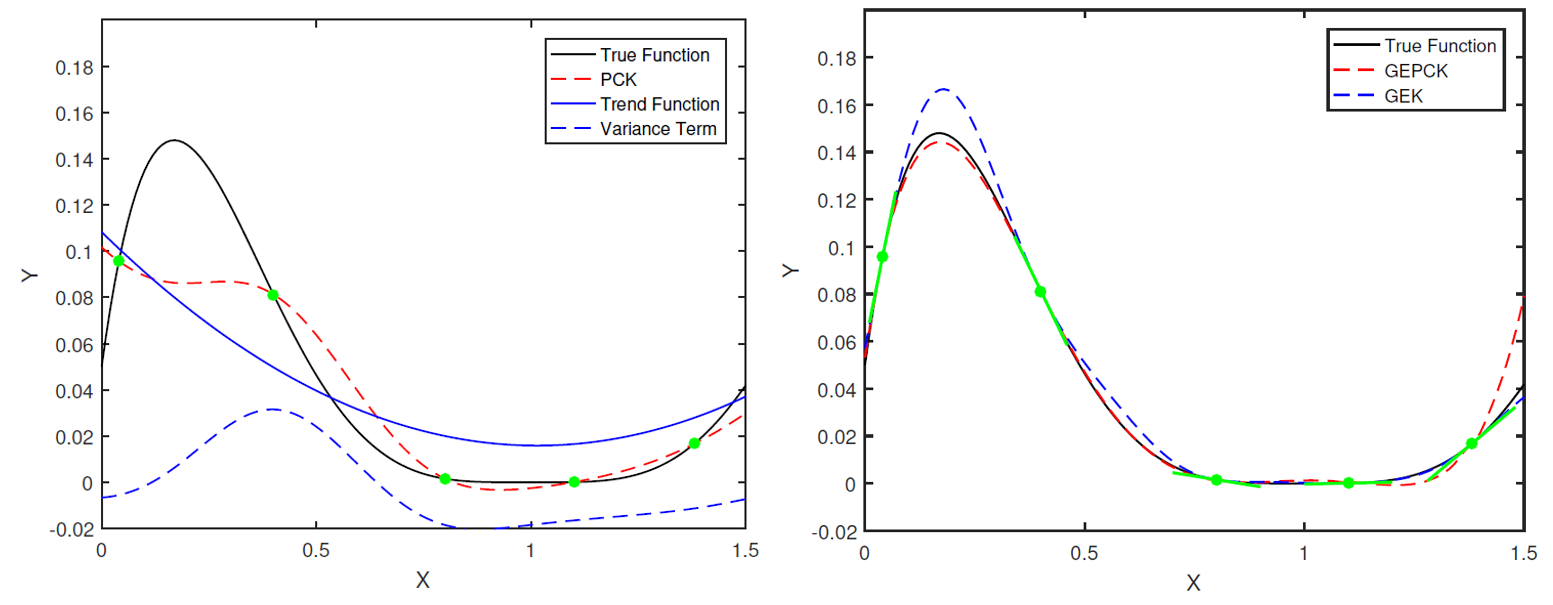
An illustration of trend function and variance term in PCK (left). GEPCK is superior to GEK in terms of approximation accuracy (right).
GE-PCK is a gradient-enhanced universal Kriging that utilizes PCE as the trend function. This technique aims to further improve the performance of gradient-enhanced Kriging (GEK) by exploiting the trend function term of Kriging via automatic basis determination. We compared the performance of GEPCK with ordinary GEK and other surrogate models on challenging analytical and real-world problems. The result shows that GEPCK consistently outperforms other surrogate models, either in terms of accuracy or robustness, for both in analytical and real test cases.
