Computer simulation has an important role in the world of engineering and science. Nowadays, real-world applications require simulations that involve complex geometries, deforming body, and moving boundaries. However, classical numerical simulations of those problems may require difficult and time-consuming mesh-generation. Therefore, the accuracy of the model heavily depends on the mesh quality. Meshless methods overcome the limitation by eliminating the mesh altogether by using a set of particles arbitrarily distributed in the domain without any interconnectivity.
Our research interest lie at the intersection of fluid mechanics and solid mechanics. In particular, the understanding of complex fluid-structure interaction found in nature-inspired flows. The broad theme of this work is to obtain mathematical models for the complex systems and develop numerical methods for the solutions of the models. We used these models and the corresponding solutions to better understand the underlying physical phenomena found in nature-inspired flow problems. This requires the development of advanced mesh-free computational methods for simulating complex fluid and solid mechanics problems.
The mesh-free Computational Fluid Dynamics (CFD) and Computational Solid Mechanics (CSM) methods that have been successfully developed are Vortex Element Method, Smooth Particle Hydrodynamics (SPH), Particle Strength Exchange (PSE), Discretization Correction Particle Strength Exchange (DC-PSE), and Least Square Moving Particle Semi-implicit Method (LSMPS). Recently our lab is more focused on the latest method, DC-PSE. Several well-established benchmark problems have been evaluated and the results are compared to those obtained in the literature.
Mesh-free Computational Fluid Dynamics: the Vortex Particle Method
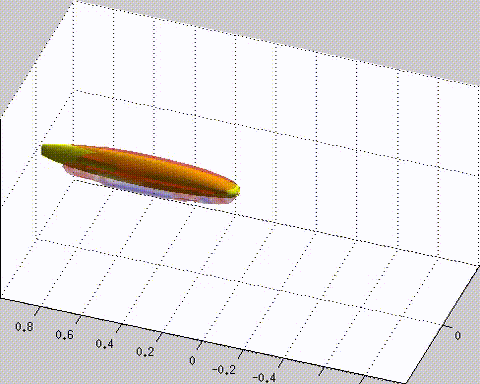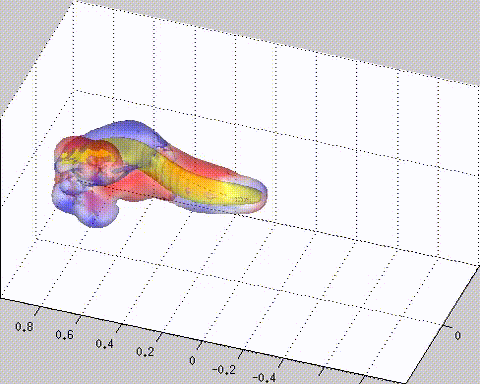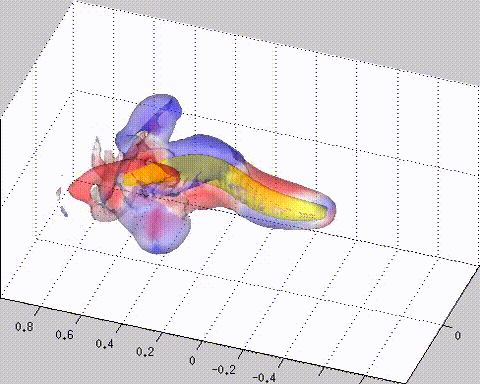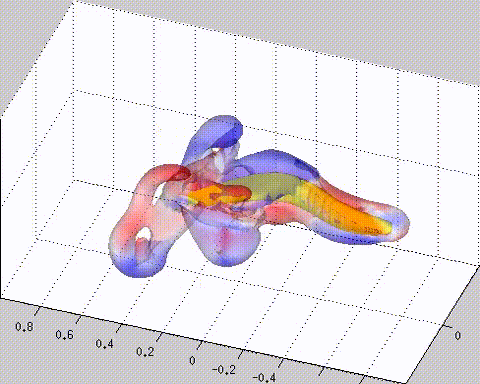
Simulation of self-propelled anguilliform swimming using Vortex Element Method.
Our group developed a mesh-free CFD method called Vortex Element Method, which is a Lagrangian Direct Numerical Simulation method for solving the Navier-Stokes equations. The vortex particle method is coupled with a current technique for boundary condition enforcement of a penalization method dealing with complex geometries. In the proposed method, we introduce particle domain and penalization domain. The first one is to compute convection with velocity evaluated by the Biot-Savart law through the fast multipole method and to evaluate diffusion by the particle strength exchange. The latter domain, in the neighborhood of the body, is to enforce wall boundary condition. We also propose the novel penalization technique by iteratively applying penalization within each time step for two-and-three-dimensional flow. This enables us for using significantly larger time step size, than what is required in the Brinkman penalization to produce high accuracy of simulation. Hence, the proposed iterative penalization can reduce computational cost while maintaining the capability of the method in handling complex geometries.
Fluid Structure Interaction Simulation using DC-PSE Based CFD and CSM Solvers.
It is well known that, due to the resolution requirements, particle methods requires large number of particles, and, therefore, are computationally expensive. Our group focused on the developments of advanced particle discritization methods. The Discretization-Corrected Particle Strength Method (DC-PSE) is developed simulations can be performed using multiresolution particle distributions. An example of fluid-structure simulations using DC PSE is shown in the Figure above. This is a full particle based simulation since both fluid and solid domains are simulated using DC PSE-based solvers.
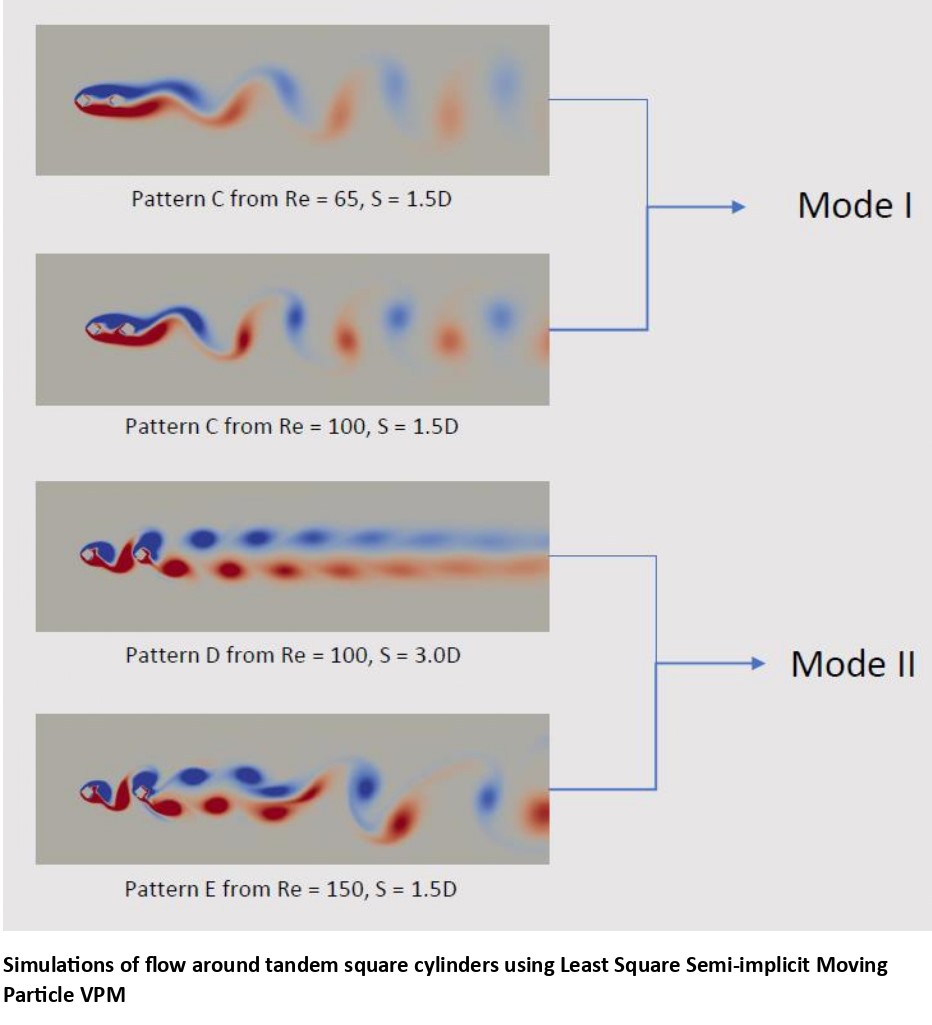
Simulation results of flow over tandem cylinders using LSMPS-based VPM Solver.
Another improvement is by utilizing the Least Square Moving Particle Semi-implicit Method (LSMPS). This method allows the use of anisoptropic self-organizing multiresolution particle distributions. Simulation of flow over tandem square cylinders, shown in the Figure above, are obtained from our current LSMPS-based VPM solver.
——————————————————————————————————————————————————
Smoothed Particle Hydrodynamics-based Computational Solid Mechanics

Crack propagation of plate with holes.
Smoothed particle hydrodynamics (SPH) is a Lagrangian and meshless method which can be applied in several fields such as astrophysics, fluid mechanics, and solid mechanics. The idea of SPH is calculate the properties of discrete particles in the support domain using smoothing function. The smoothing function determine the effect of neighboring particles which interact to each other. In this project, we developed two versions of SPH: Total Lagrangian Formulation SPH and Updated Lagrangian Formulation SPH to simulate three dimensional elastodynamics and fracture mechanics problems.
——————————————————————————————————————————————————
Fully Kinetic Simulations with LSMPS for Rarefied Gas Dynamics Simulations
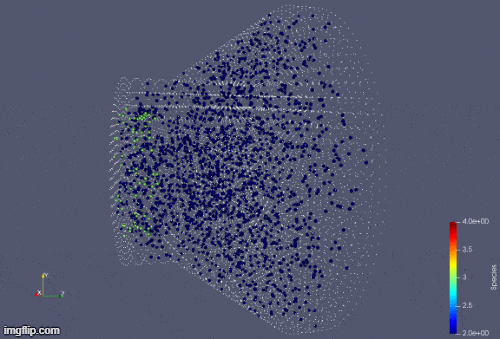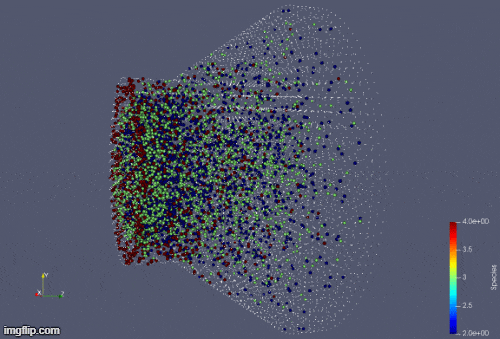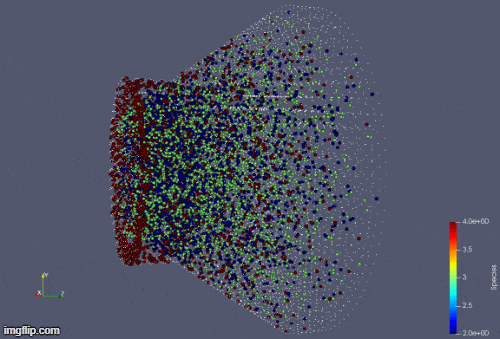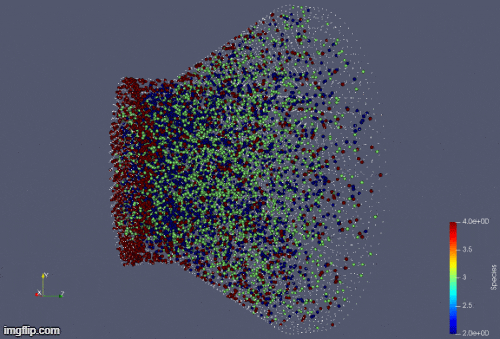
Plasma Simulation inside Hall Thruster.
We also develop computational methods for three-dimensional simulation of plasma (ions, electrons, and neutrals) and rarefied gas using particle/meshless methods. In plasma simulation, the value of electric field and magnetic field are calculated by solving the Gauss Law for electric field and magnetic field. Particle based spatial derivatives are calculated using Least Squares Moving Particle Semi-implicit (LSMPS). Collision terms are computed using Direct Simulation Monte Carlo (DSMC) method.
——————————————————————————————————————————————————
The Lattice Bolzmann Method
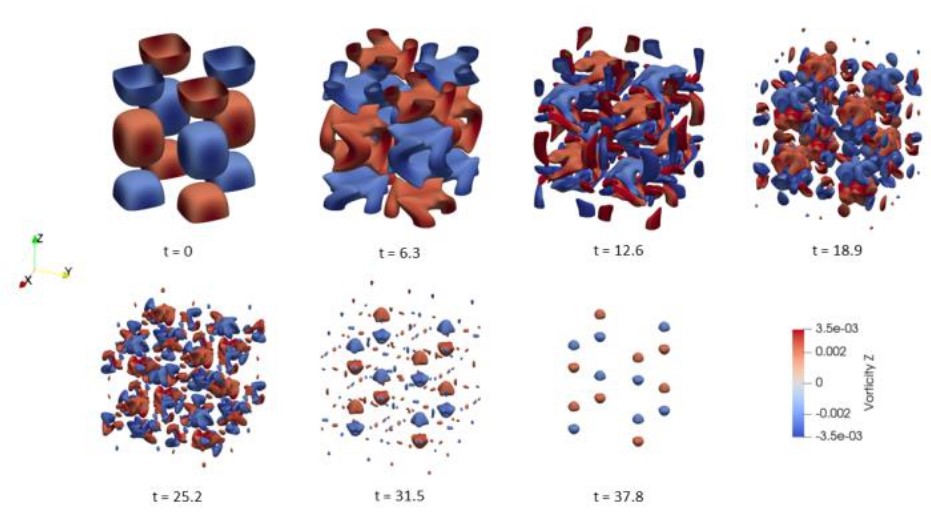
Decay of Taylor-Green Vortices, simulated using Lattice Boltzmann Methotd (LBM).
Another particle/meshless methods that is being developed in our lab is the Lattice Boltzmann Method (LBM). Instead of solving Navier-Stokes equation, LBM solves the Boltzmann equation, which is the governing equation for kinetic theory of gasses. It is a mesoscale computational method which is in between the conventional continuum CFD computation (macroscale) and molecular dynamics (microscale). In our group, LBM is developed for multicomponent/multiphase fluid, nano fluid, and rarefied gas dynamics simulations purposes. The Figure above shows the detail the decaying process of Taylor-Green vortices simulated with our latest LBM-based CFD solver.
